Il est demandé de trouver toutes les fonctions , à valeurs réelles et définies sur un intervalle ouvert
où elles sont deux fois continûment dérivables, qui sont telles que, dans
,
- Commentaire
- Reblog
-
Souscrire
Abonné
Vous disposez déjà dʼun compte WordPress ? Connectez-vous maintenant.
Ca sent l’exponentielle ce truc 😉 D’ailleurs, en notant ce que donne (u/u’)’, il me semble bien avoir la solution…
En effet, cela « sent l’exponentielle ». Je considérerais plutôt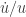 mais le problème — pour autant qu’il y en ait un — c’est qu’on doit alors supposer que
mais le problème — pour autant qu’il y en ait un — c’est qu’on doit alors supposer que  n’a aucun zéro. La (petite) difficulté de la question réside là. Mais vous y avez peut-être déjà songé, et règlé le problème. A vous lire …
n’a aucun zéro. La (petite) difficulté de la question réside là. Mais vous y avez peut-être déjà songé, et règlé le problème. A vous lire …
J’y ai songé de la manière suivante : soit u est nul sur tout l’intervalle, ce qui donne une solution triviale u = 0 à la question, soit u est nul sur un ensemble discrêt de points. Dans ce cas, je considère l’équation sur n’importe quel intervalle qui ne comprend aucun zéro, ce qui donne u = a exp (b x), avec a != 0. Comme c’est la seule forme possible de solution non-nulle sur cet intervalle a priori quelconque, on en déduit qu’elle est valable dans |R (u et toutes ses dérivées sont de signes constant).
«soit u est nul sur tout l’intervalle […] soit u est nul sur un ensemble discrêt de points»
Bonjour,
Pourquoi l’ensemble des zéros de u ne pourrait-il pas être autrement que discret ou égal à tout l’intervalle ?
Bonjour, oui, c’est vrai que la fonction n’est a priori que deux fois continûment dérivable, donc on pourrait supposer des sous-intervalles continus de I où u est nulle et où elle est non-nulle dans l’un ou l’autre sous-intervalle contigu, avec aux bornes (par exemple, u(x) est nulle lorsque x est inférieur ou égal à 0, et est un polynôme dont tous les termes sont une puissance de x supérieure ou égale à 3 lorsque x est positif). Une formulation plus précise serait donc « soit u est nulle sur tout l’intervalle, soit il existe au moins un sous-intervalle continu de I dans lequel u est non-nulle ».
aux bornes (par exemple, u(x) est nulle lorsque x est inférieur ou égal à 0, et est un polynôme dont tous les termes sont une puissance de x supérieure ou égale à 3 lorsque x est positif). Une formulation plus précise serait donc « soit u est nulle sur tout l’intervalle, soit il existe au moins un sous-intervalle continu de I dans lequel u est non-nulle ».
Merci beaucoup. Cela semble coller. Je dis semble car je ne comprends pas très bien la dernière phrase.
Ma méthode est fort proche. En ce qui me concerne, lorsque n’est pas nul dans son domaine de définition
n’est pas nul dans son domaine de définition 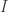 , je considère une composante connexe de l’ensemble des points en lesquels
, je considère une composante connexe de l’ensemble des points en lesquels  ne s’annule pas. C’est un intervalle
ne s’annule pas. C’est un intervalle  dont je démontre qu’il coïncide avec
dont je démontre qu’il coïncide avec 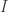 . D’abord, comme vous, j’arrive à la conclusion que, dans
. D’abord, comme vous, j’arrive à la conclusion que, dans  ,
,  est un multiple non nul d’une exponentielle. Ensuite, par l’absurde, si une borne de
est un multiple non nul d’une exponentielle. Ensuite, par l’absurde, si une borne de  se trouve dans
se trouve dans 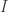 alors on a une contradiction : la limite de
alors on a une contradiction : la limite de  en cette borne doit à la fois être nulle et non nulle, car la borne en question est limite de zéros de
en cette borne doit à la fois être nulle et non nulle, car la borne en question est limite de zéros de  .
.
Pour être clair, cette réponse réfère à la seconde intervention de MR.
J’adhère à la formulation de notre hôte. Je vais encore paraphraser pour me sentir totalement convaincu : soit une solution non-identiquement nulle et
une solution non-identiquement nulle et  une composante connexe où
une composante connexe où  est non-nulle. En considérant
est non-nulle. En considérant  l’infimum de
l’infimum de  , alors
, alors
par continuité, or la limite à droite est non-nulle (car sur ,
,  est *une* exponentielle, fixée, donc on calcule la limite explicitement, et qui ne vaut pas
est *une* exponentielle, fixée, donc on calcule la limite explicitement, et qui ne vaut pas  ). On en déduit que
). On en déduit que 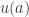 est non-nulle, d’où
est non-nulle, d’où  est non nulle sur un voisinage de
est non nulle sur un voisinage de  (continuité), donc
(continuité), donc  n’était pas l’infimum de
n’était pas l’infimum de  .
.
Je confirme : je suis convaincu. Merci d’avoir mis des mots sur cet argument !
C’est moi qui vous remercie pour cette « paraphrase »! 🙂
En conclusion, la réponse à la question est : les fonctions en question sont les applications
où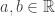 .
.