La droite (DE) coupe deux côtés distincts du triangle, disons [AB] et
[AC], en deux points distincts, disons F sur [AB] et G sur [AC].
Alors on a DE < FG. Notons D (resp. D') la droite orthogonale à FG
et passant par F (resp. G).
Maintenant supposons que FG > AB et FG > AC ; le but est de montrer
qu’on a alors FG < BC. Les droites parallèles D et D' partagent le
plan en trois parties : une bande et deux demi-plans.
La bande contient le point A (car FG>AB>AF et FG>AC>AG), et chacun des
demi-plans contient l’un des points B ou C. Il vient alors que BC > FG.
J’achète. C’est subtil comme preuve et cela repose sur des phénomènes non triviaux du genre une droite passant par un point intérieur coupe la frontière d’un convexe en deux points et d’autres relatifs à l’orthogonalité. Ma preuve, légèrement différente, repose aussi sur ces mêmes propriétés.
Comme le laisse entendre PB, c’est une évidence dont il faut se méfier.
En ce qui me concerne, avec les notaions de MathOMan, je fais glisser F vers le sommet A ou B qui l’écarte du pied de la projection orthogonale de G sur (AB), ce qui augmente GF. Si ce sommet est A, je fais alors glisser G vers C et on a EF < AC, si c'est B, alors je fais glisser G vers le sommet A ou C qui l'écarte le plus du pied de la hauteur issue de B, ce qui montre de nouveau que EF est moindre qu'un des côtés du triangle.
Lemme 1 (très élémentaire). Une fonction avec , réels, définie sur un segment , n’atteint pas son maximum en un point intérieur à .
Lemme 2 (conséquence immédiate du lemme 1). Si est un point du plan et si est un point qui parcourt un segment , alors la distance ne prend pas sa valeur maximale en un point intérieur à .
Lemme 3 (diamètre d’un polygone convexe (et compact)). Le diamètre d’un polygone convexe est atteint pour certains sommets et de .
Sauf erreur, le lemme 3 est une conséquence immédiate du lemme 2. Et le lemme 3 répond à la question car tout triangle est un polygone convexe 🙂
De manière plus compacte : soit un convexe compact (par exemple l’intérieur d’un triangle). L’application de dans définie par est convexe (comme composée d’une application linéaire et d’une application convexe) donc atteint son maximum en un point extrémal.
Cela semble évident mais… il faut l’écrire. Je vais réfléchir pendant mes vacances 🙂
La droite (DE) coupe deux côtés distincts du triangle, disons [AB] et
[AC], en deux points distincts, disons F sur [AB] et G sur [AC].
Alors on a DE < FG. Notons D (resp. D') la droite orthogonale à FG
et passant par F (resp. G).
Maintenant supposons que FG > AB et FG > AC ; le but est de montrer
qu’on a alors FG < BC. Les droites parallèles D et D' partagent le
plan en trois parties : une bande et deux demi-plans.
La bande contient le point A (car FG>AB>AF et FG>AC>AG), et chacun des
demi-plans contient l’un des points B ou C. Il vient alors que BC > FG.
J’achète. C’est subtil comme preuve et cela repose sur des phénomènes non triviaux du genre une droite passant par un point intérieur coupe la frontière d’un convexe en deux points et d’autres relatifs à l’orthogonalité. Ma preuve, légèrement différente, repose aussi sur ces mêmes propriétés.
Comme le laisse entendre PB, c’est une évidence dont il faut se méfier.
😉
En ce qui me concerne, avec les notaions de MathOMan, je fais glisser F vers le sommet A ou B qui l’écarte du pied de la projection orthogonale de G sur (AB), ce qui augmente GF. Si ce sommet est A, je fais alors glisser G vers C et on a EF < AC, si c'est B, alors je fais glisser G vers le sommet A ou C qui l'écarte le plus du pied de la hauteur issue de B, ce qui montre de nouveau que EF est moindre qu'un des côtés du triangle.
Bonjour, j’essaye quelque chose :
Lemme 1 (très élémentaire). Une fonction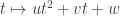 avec
avec  ,
, 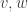 réels, définie sur un segment
réels, définie sur un segment ![[a.b]](https://s0.wp.com/latex.php?latex=%5Ba.b%5D&bg=ffffff&fg=323232&s=0&c=20201002) , n’atteint pas son maximum en un point intérieur à
, n’atteint pas son maximum en un point intérieur à ![[a,b]](https://s0.wp.com/latex.php?latex=%5Ba%2Cb%5D&bg=ffffff&fg=323232&s=0&c=20201002) .
.
Lemme 2 (conséquence immédiate du lemme 1). Si est un point du plan et si
est un point du plan et si  est un point qui parcourt un segment
est un point qui parcourt un segment ![[A,B]](https://s0.wp.com/latex.php?latex=%5BA%2CB%5D&bg=ffffff&fg=323232&s=0&c=20201002) , alors la distance
, alors la distance 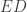 ne prend pas sa valeur maximale en un point intérieur à
ne prend pas sa valeur maximale en un point intérieur à ![[A,B]](https://s0.wp.com/latex.php?latex=%5BA%2CB%5D&bg=ffffff&fg=323232&s=0&c=20201002) .
.
Lemme 3 (diamètre d’un polygone convexe (et compact)). Le diamètre d’un polygone convexe
d’un polygone convexe 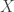 est atteint pour certains sommets
est atteint pour certains sommets 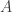 et
et 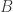 de
de 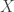 .
.
Sauf erreur, le lemme 3 est une conséquence immédiate du lemme 2. Et le lemme 3 répond à la question car tout triangle est un polygone convexe 🙂
C’est une belle preuve, avec des arguments originaux.
Merci!
De manière plus compacte : soit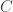 un convexe compact (par exemple l’intérieur d’un triangle). L’application de
un convexe compact (par exemple l’intérieur d’un triangle). L’application de  dans
dans  définie par
définie par  est convexe (comme composée d’une application linéaire et d’une application convexe) donc atteint son maximum en un point extrémal.
est convexe (comme composée d’une application linéaire et d’une application convexe) donc atteint son maximum en un point extrémal.
C’est effectivement expéditif! Bravo!