Je consigne ici une leçon que je donne régulièrement dans un cours d’introduction à la géométrie différentielle. Elle intrigue les étudiants qui, le plus souvent, l’aime beaucoup.
Il s’agit de retrouver les lois de Snell-Descartes à partir du principe de Fermat selon lequel le chemin suivi par la lumière rend stationnaire le temps de parcours. Dans un milieu homogène, sa vitesse est constante et elle suit donc des segments de droites.
La question est de savoir comment est modifiée sa trajectoire lorsqu’elle traverse la surface (*) séparant deux milieux homogènes dans lesquels elle circule à des vitesses différentes (lois de la réfraction) ou lorsqu’elle se réfléchit en un point de
(lois de la réflexion).
Dans le premier cas, un rayon lumineux issu d’une source ponctuelle placée dans le premier milieu traverse
en
et poursuit sa trajectoire jusqu’en un point cible
du second.
Dans le second, est le point en lequel le rayon se réfléchit vers la cible et celle-ci est dans le même milieu que la source.
Dans les deux cas, le temps mis pour joindre et
via un point
est
où est la vitesse de la lumière avant l’incidence et
après (on a donc
en cas de réflexion).
Par hypothèse, est stationnaire en
. Par conséquent, d’après la règle des multiplicateurs de Lagrange, le gradient de
en
,
est normal à en
. Nous en déduisons une première loi :
Le rayon incident,
, le rayon réfracté (ou réfléchi),
, et la normale au point d’incidence à la surface de séparation sont dans un même plan.
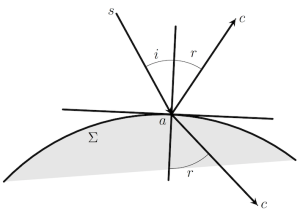
Ce plan coupe la surface selon une courbe et le plan tangent de
en
selon une droite, tangente à la courbe, comme illustré sur le dessin suivant.
En exprimant que le produit scalaire de avec un vecteur directeur unitaire de cette droite est nul, on voit facilement, avec les notations de la figure, que
C’est la seconde loi de Snell-Descartes.
Dans le cas de la réflexion, ; elle exprime donc le fait que l’angle de réflexion est égal à l’angle d’incidence.
Pour la réfraction, et donc
et
sont différents. Il peut même arriver que
soit égal à
. On parle alors de réflexion totale ou d’incidence rasante. L’angle d’incidence correspondant est alors donné par
Le phénomène ne se présente donc que si .
D’habitude, j’achève la leçon par une application amusante du phénomène de réflexion totale.
Il s’agit de déterminer en quel point du rivage doit accoster un bonhomme qui quitte l’îlot
en canot afin de se rendre au plus vite dans sa maison
située sur le rivage, sachant que sur l’eau, il canote à deux km/h et qu’il marche le long du rivage à quatre km/h.
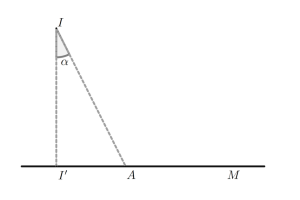
Les données du problèmes sont représentées sur ce dessin, où est la projection orthogonale de
sur le rivage, supposé rectiligne.
En fait, comme il s’agit de minimiser le temps de parcours, le bonhomme doit suivre le trajet d’un rayon lumineux émis depuis et formant l’angle d’incidence correspondant à l’incidence rasante. Un tel rayon existe car la vitesse
du bonhomme dans l’eau est plus petite que sa vitesse
sur terre. D’après ce qui précède, l’angle
est donné par
de sorte que
et le problème est résolu.
Notez que si le bonhomme se déplaçait plus vite sur l’eau que sur terre (par exemple en utilisant un Jet Ski 😉 ) alors le trajet le plus rapide consisterait à aller directement en ligne droite de l’îlot à sa maison.
P.S. En fait, la solution du petit problème donnée ci-dessus n’est correcte que si est assez éloigné de
, c’est-à-dire si le point
est entre
et
. J’aurais dû le mentionner d’emblée. Je vais bientôt revenir sur cette observation dans un prochain billet. P.L. 30/04/2016
__________
(*) Nous supposons que est une variété plongée (dans
).
Bonjour Pierre. Merci pour cet article sur un sujet cher aux physiciens. Mais où sont les multiplicateurs de Lagrange mentionnés dans le titre? Il me semble qu’il s’agit d’un simple problème d’optimisation et je ne vois pas où est la contrainte.
Bonsoir ThM! C’est la restriction de à
à  qui est stationnaire. La contrainte est donc l’équation cartésienne
qui est stationnaire. La contrainte est donc l’équation cartésienne 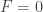 de
de  au voisinage du point stationnaire. Comme celle-ci est scalaire, il n’y a qu’un « multiplicateur indéterminé de Lagrange » ce qui signifie que le gradient de
au voisinage du point stationnaire. Comme celle-ci est scalaire, il n’y a qu’un « multiplicateur indéterminé de Lagrange » ce qui signifie que le gradient de  en
en  est un multiple de celui de
est un multiple de celui de 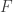 . Or ce dernier est normal à la surface en
. Or ce dernier est normal à la surface en  , ce qui permet de conclure.
, ce qui permet de conclure.
De façon générale, l’observation de Lagrange est qu’en un point stationnaire de la restriction d’une fonction
de la restriction d’une fonction 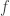 à une variété plongée
à une variété plongée 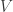 de
de  , le gradient de la fonction est perpendiculaire à l’espace tangent de
, le gradient de la fonction est perpendiculaire à l’espace tangent de 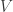 en
en  (c’est à peu près évident : cela signifie que les dérivées de la fonction dans les directions tangentes à la variété sont nulles; transversalement, on n’a aucun renseignement puisque seule la restriction de la fonction à la variété est prise en compte), ce qui équivaut au fait que ce gradient est une combinaison linéaire des gradients en
(c’est à peu près évident : cela signifie que les dérivées de la fonction dans les directions tangentes à la variété sont nulles; transversalement, on n’a aucun renseignement puisque seule la restriction de la fonction à la variété est prise en compte), ce qui équivaut au fait que ce gradient est une combinaison linéaire des gradients en  d’un jeu d’équations cartésiennes définissant la variété au voisinage de
d’un jeu d’équations cartésiennes définissant la variété au voisinage de  — les contraintes. Les coefficients de cette combinaison linéaire sont les fameux « multiplicateurs indéterminés » de Lagrange.
— les contraintes. Les coefficients de cette combinaison linéaire sont les fameux « multiplicateurs indéterminés » de Lagrange.
Merci pour la réponse. C’est assez évident en effet, il est toujours bien de penser à l’interprétation géométrique des méthodes analytiques. t est une fonction du point intermédiaire x qui est sur la surface Sigma, et on veut que t soit stationnaire.
Pingback: A propos d’un problème d’optimisation « élémentaire | «Blog de Pierre Lecomte