Voici une jolie identité. Elle est peut être immédiate, je n’y ai pas trop réfléchi. En tout cas, elle ne devrait pas vous résister très longtemps. Elle vaut pour tout entier positif 
-
Suivre
Abonné
Vous disposez déjà dʼun compte WordPress ? Connectez-vous maintenant.
Blog de Pierre Lecomte 
Elle est effectivement fort simple à prouver … 😉
Je l’ai d’abord obtenue par un moyen détourné quoique rapide. Mais il s’avère a posteriori qu’elle est facile à établir directement.
En effet, directement : on peut vérifier que
et après c’est gagné, par exemple avec la formule du binôme.
C’est en effet le plus simple. Ma première méthode, en fait : le calcul m’ayant conduit à l’identité, consiste à appliquer la formule du binôme à
puis, dans chaque terme, aux puissances de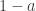 
, et à identifier le coefficient de 
.
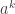Pour aller plus loin avec cette identité : On l’utilise pour établir la formule d’inversion de Pascal, puis pour calculer diverses nombres, comme le nombre de surjections d’un ensemble sur un autre. Par exemple, voir l’exercice 1.29 et sa solution dans le poly (en cours)
Cliquer pour accéder à agreg-int-orsay-2012-poly.pdf
Je ne connaissais pas cette formule d’inversion; c’est fort intéressant! Merci pour ce commentaire.