J’ai obtenu par hasard la formule suivante que je vous propose de démontrer pour vous divertir. Elle est tombée comme un fruit mûr lorsque je faisais certains calculs qui ne la concernaient pas. Elle est peut-être facile à prouver directement. Je n’en sais rien, je n’ai pas vraiment essayé de le faire. La voici
Les nombres et
sont des entiers positifs ou nuls.
Bon amusement! 😉
C’est une somme télescopique grâce à la formule d’addition. Sinon, on peut aussi compter le nombre de parties à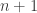 éléments de l’ensemble
éléments de l’ensemble ![[1,n+k+1]](https://s0.wp.com/latex.php?latex=%5B1%2Cn%2Bk%2B1%5D&bg=ffffff&fg=323232&s=0&c=20201002) en distinguant ces parties suivant la valeur de leur maximum (un entier de la forme
en distinguant ces parties suivant la valeur de leur maximum (un entier de la forme 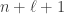 avec
avec  entre
entre  et
et 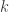 )
)
Merci JeanN mais je ne comprends pas immédiatement. Pourriez vous expliciter? D’avance merci!
On fixe entre
entre  et
et 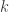
![[1,n+k+1]](https://s0.wp.com/latex.php?latex=%5B1%2Cn%2Bk%2B1%5D&bg=ffffff&fg=323232&s=0&c=20201002) à
à 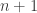 éléments dont le maximum est
éléments dont le maximum est 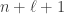 .
.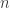 éléments entre
éléments entre 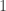 et
et  donc
donc 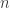 parmi
parmi  possibilités.
possibilités. décrit
décrit ![[0,k]](https://s0.wp.com/latex.php?latex=%5B0%2Ck%5D&bg=ffffff&fg=323232&s=0&c=20201002) , on compte sans redondance toutes les parties de
, on compte sans redondance toutes les parties de ![[1,n+k+1]](https://s0.wp.com/latex.php?latex=%5B1%2Cn%2Bk%2B1%5D&bg=ffffff&fg=323232&s=0&c=20201002) à
à 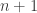 éléments (et il y en a
éléments (et il y en a 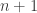 parmi
parmi  )
)
On cherche à compter le nombre de parties de
Pour construire une telle partie, il suffit de choisir
Lorsque
D’où le résultat par unicité du cardinal.
C’est joli, merci! 🙂