Afin de ne pas le perdre de vue, je reformule ici un problème posé dans ce premier commentaire.
Dans la figure ci-dessus, le pentagone est régulier et
Il est demandé de calculer le rapport du périmètre de à celui de
.
Lorsqu’on fait , ce problème se réduit à celui posé dans le billet sur lequel porte le commentaire.
Bon amusement!
😉
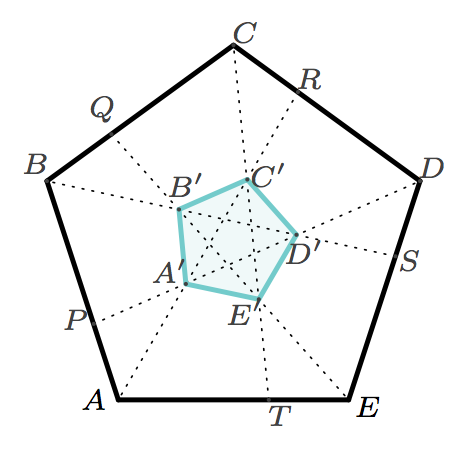
Pardon de revenir à la charge mais ce n’est pas tout à fait la configuration de Cremona-Richmond. Dans celle-ci, les deux pentagones sont homothétiques (ici, l’intérieur est un peu «penché»). Si on redresse ceux de la figure ci-dessus de sorte que (B’D’) devienne parallèle à (AE), que l’on appelle comme ici S l’intersection de (B’D’) avec (DE), on a une contrainte supplémentaire : l’alignement de S, C’ et B. Il n’y a qu’une seule valeur du rapport B’C’/BC qui permette cet alignement (et la question est de trouver ce rapport).
Vous faites bien de me corriger! Merci! En fait, j’avais mal compris la question, et mal analysé la figure donnée dans cette référence. A vrai dire, je ne vois toujours pas comment construire la configuration de Cremona-Richmond, c’est-à-dire les segments mauves af-bc, etc. de la figure présentée sur cette page, construction qui n’y est pas explicitée. Finalement, c’est précisément l’objet de votre question.
Bon, j’ai une méthode et elle devrait être relativement simple à mettre en oeuvre. J’ai fait une partie des calculs et il me reste encore un petit bout de chemin à faire. Malheureusement, je n’ai plus trop de temps pour cela. J’espère la semaine prochaine.
J’explique la démarche. Je n’ai pas encore achevé les calculs mais voici au moins les idées rendant les choses opérationnelles.
La question est de trouver le rapport d’une homothétie centrée au centre de gravité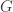 du pentagone
du pentagone 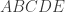 et qui donne de celui-ci une image
et qui donne de celui-ci une image  vérifiant les conditions d’alignement décrites par Jer anonyme, conditions qu’on peut traduire en disant qu’il faut que les droites
vérifiant les conditions d’alignement décrites par Jer anonyme, conditions qu’on peut traduire en disant qu’il faut que les droites  aient un point commun.
aient un point commun.
Ces conditions sont purement affines. Par conséquent, il suffit de calculer le rapport en question pour un pentagone affine régulier convexe particulier. En l’occurrence, je choisis le pentagone affine régulier convexe de pour lequel
pour lequel
Avec ce choix, les coordonnées de l’image d’un point par une homothétie de centre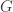 sont très simples à calculer. Pour rappel, le pentagone
sont très simples à calculer. Pour rappel, le pentagone 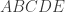 est affine régulier convexe si, et seulement si,
est affine régulier convexe si, et seulement si,
Comme on le vérifie facilement, les relations (3) et (4) impliquent les autres. On utilise alors ces deux relations pour calculer les points à l’aide de
à l’aide de 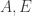 et
et 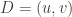 . Les coordonnées de ce derniers sont ensuite trouvées en imposant que le centre de gravité du pentagone soit l’origine. Voici ce que les calculs donnent
. Les coordonnées de ce derniers sont ensuite trouvées en imposant que le centre de gravité du pentagone soit l’origine. Voici ce que les calculs donnent
Il est ensuite facile d’écrire les images de ces trois points par l’homothétie de centre
de ces trois points par l’homothétie de centre 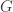 et de rapport
et de rapport 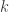 : il suffit de multiplier leurs coordonnées par ce nombre. On peut alors trouver des équations cartésiennes pour les droites
: il suffit de multiplier leurs coordonnées par ce nombre. On peut alors trouver des équations cartésiennes pour les droites  puis exiger que celles-ci soient concourantes en annulant un certain déterminant (noter que l’équation pour la seconde droite est a priori très simple puisqu’elle est parallèle à
puis exiger que celles-ci soient concourantes en annulant un certain déterminant (noter que l’équation pour la seconde droite est a priori très simple puisqu’elle est parallèle à  ).
).
Cela donne une équation du second degré en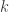 . Je ne l’ai pas encore écrite proprement. C’est un peu longuet et j’hésite entre me retrousser les manches et faire travailler un esclave qu’il faudrait alors programmer pour qu’il calcule bien dans
. Je ne l’ai pas encore écrite proprement. C’est un peu longuet et j’hésite entre me retrousser les manches et faire travailler un esclave qu’il faudrait alors programmer pour qu’il calcule bien dans ![\mathbb Q[\varphi]](https://s0.wp.com/latex.php?latex=%5Cmathbb+Q%5B%5Cvarphi%5D&bg=ffffff&fg=323232&s=0&c=20201002) . Cela dit, le nombre d’or a certes des propriétés très riches. J’ai quand même un doute : je ne suis pas certain qu’on obtiendra une valeur raisonnablement simple pour le rapport de l’homothétie cherchée.
. Cela dit, le nombre d’or a certes des propriétés très riches. J’ai quand même un doute : je ne suis pas certain qu’on obtiendra une valeur raisonnablement simple pour le rapport de l’homothétie cherchée.
P.S. Le nombre d’or désigné ici par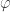 est noté
est noté  dans le billet auquel j’ai fait référence plus haut, pour ne pas entrer en conflit avec la notation traditionnelle de l’indicatrice d’Euler.
dans le billet auquel j’ai fait référence plus haut, pour ne pas entrer en conflit avec la notation traditionnelle de l’indicatrice d’Euler.
Pour faire les calculs, j’ai appliqué cette stratégie mais dans un autre système de coordonnées. Quitte à faire un peu tourner le pentagone extérieur, on peut supposer que ses sommets sont les où
où  et
et  décrit
décrit 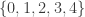 . Les sommets du pentagone extérieurs sont alors les
. Les sommets du pentagone extérieurs sont alors les 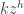 (avec les mêmes
(avec les mêmes  ). On cherche
). On cherche 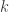 de sorte que les droites reliant
de sorte que les droites reliant 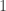 et
et  d’une part,
d’une part, 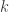 et
et  d’autre part,
d’autre part, 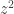 et
et  enfin soient concourantes. Comme le dit Pierre, cela s’exprime par l’annulation d’un déterminant
enfin soient concourantes. Comme le dit Pierre, cela s’exprime par l’annulation d’un déterminant 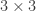 .
.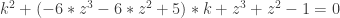 . Les coefficients et les deux racines de cette équation sont réelles. La seule qui est positive vaut
. Les coefficients et les deux racines de cette équation sont réelles. La seule qui est positive vaut
Tous calculs faits (avec un ordinateur), on obtient :
ce qui est visiblement — à nouveau, comme l’a dit Pierre — la solution d’une équation de degré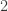 à coefficients dans
à coefficients dans ![\mathbb{Q}[\varphi]](https://s0.wp.com/latex.php?latex=%5Cmathbb%7BQ%7D%5B%5Cvarphi%5D&bg=ffffff&fg=323232&s=0&c=20201002) .
.
Merci beaucoup! C’est plus simple avec les racines cinquièmes de l’unité. Je finirai mes calculs pour vérifier qu’ils aboutissent bien à la même réponse.