A propos des empilements infinis de radicaux III

Je présente dans ce billet ce que je sais de la fonction $e_{a,b}$ introduite dans le billet précédent pour étudier les empilements infinis de radicaux. J’utiliserai ici librement les notations de ce billet. Pour rappel, les suites $a$ et $b$ sont désormais à valeurs strictement positives.

Préambule

Avant d’entrer dans le vif du sujet, je voudrais introduire une famille de fonctions bien utiles. Il s’agit de la suite de fonctions $\xi_n :[0,+\infty[ \to [0,+\infty[$ définie par récurrence par

$\begin{cases}\xi_0(x)=x\\[1ex]\xi_{n+1}(x)=\xi_n(\sqrt{a_n+b_nx})\end{cases}$

Voici les valeurs des premiers $\xi_n$ :

$\xi_0(x)=x, \quad \xi_1(x)=\sqrt{a_0+b_0x}, \quad \xi_2(x)=\sqrt{a_0+b_0\sqrt{a_1+b_1x}}, \quad \ldots$

Bien que, pour ne pas alourdir l’écriture, le nom de ces fonctions ne fasse pas explicitement référence aux suites $a$ et $b$ , elles en dépendent bel et bien. Nous aurons besoin des fonctions relatives aux suites décalées $k$ fois $\sigma^k(a)$ et $\sigma^k(b)$ . Nous conviendrons de les désigner par $\xi_n^{\sigma^k}$ . Par exemple,

$\xi_2^{\sigma^3}(x)=\sqrt{a_3+b_3\sqrt{a_4+b_4x}}$

Voici une propriété que nous utiliserons plus bas.

(1) $\boxed{\forall n\in\mathbf N, \quad \xi_{n+1}(x)=\sqrt{a_0+b_0\xi_n^\sigma(x)}}$

Elle se démontre par récurrence. Je fais l’induction, le cas de base étant immédiat. En supposant la propriété vraie pour une certaine valeur $p$ de $n$ , il vient

$\begin{array}{rcl}\xi_{p+2}(x)&=&\xi_{p+1}(\sqrt{a_{p+1}+b_{p+1}x})\\[1ex]&=&\sqrt{a_0+b_0\xi_p^\sigma(\sqrt{a_{p+1}+b_{p+1}x})}\\[1ex]&=&\sqrt{a_0+b_0\xi_{p+1}^\sigma(x)}\end{array}$

Notons au passage une autre propriété où la notation $\xi_n^{\sigma^k}$ s’avère bien utile. Elle nous donne les dérivées des $\xi_n$ et nous montre, si besoin en était, que les fonctions $\xi_n$ sont strictement croissantes.

$\boxed{\forall n>0, \quad \xi_n'=\frac{b_0\cdots b_{n-1}}{2^n\xi_n\xi_{n-1}^\sigma\cdots\xi_1^{\sigma^{n-1}}}}$

Elle se démontre facilement par récurrence mais je ne le fais pas ici.

Un des intérêts des fonctions $\xi_n$ réside en ceci : si la suite $c$ est à valeurs positives ou nulles, alors

(2) $\boxed{\forall n\in\mathbf N,\quad u_n(c)=\xi_n(c_n)}$

Un théorème

Voici le résultat principal de ce billet. J’ai rappelé plus haut que les suites $a$ et $b$ sont à valeurs strictement positives mais je le répète dans l’énoncé pour bien mettre en évidence ses hypothèses.

Si les suites $a$ et $b$ sont à valeurs strictement positives, alors

1) $\mathbf 0\in \mathscr{D}_{a,b}$

2) La limite $\gamma_0$ de $u(\mathbf 0)$ est un nombre réel, si, et seulement si, il existe une suite $c\in \mathscr{D}_{a,b}$ telle que $u(c)$ soit constant.

3) Si $\gamma_0$ est un nombre réel et si $\gamma\geqslant \gamma_0$ , alors il existe une seule suite $c\in \mathscr{D}_{a,b}$ telle que les $u_n(c)$ valent tous $\gamma$ .

Voici ce que je vous propose en guise de preuve.

Considérons une suite $c:\mathbf N\to [0,+\infty[$ et demandons-nous à quelles conditions $u(c)$ est constant. Vu (2), $u_{n+1}(c)=u_{n}(c)$ si, et seulement si,

$\xi_{n+1}(c_{n+1})=\xi_n(\sqrt{a_n+b_nc_{n+1}})=\xi_n(c_n)$

Mais $\xi_n$ est injectif. Cela équivaut donc à $\sqrt{a_n+b_nc_{n+1}}=c_n$ et finalement à, puisque $c_n\geqslant 0$ ,

$c_{n+1}=\cfrac{c_n^2-a_n}{b_n}$

La suite $c$ est donc complètement déterminée par sa première valeur $c_0$ .

J’affirme alors que, étant donné $\gamma\geqslant 0$ , la suite $c$ définie par récurrence par

(3) $\begin{cases}c_0=\gamma\\[3ex] c_{n+1}=\cfrac{c_n^2-a_n}{b_n}\end{cases}$

est à valeurs positives ou nulles si, et seulement si,

(4) $\forall n\in\mathbf N,\quad \gamma\geqslant u_n(\mathbf 0)$

Montrons d’abord que si (4) est vérifié alors les valeurs de $c$ ne sont pas négatives.
Nous allons voir, plus précisément, que si $\gamma\geqslant u_n(\mathbf 0)$ , alors $c_0,\ldots,c_n\geqslant 0$ , ce qui suffit.

Partons de

$c_0=\gamma\geqslant u_n(\mathbf 0)=\xi_n(0)$

Vu (1), que nous allons utiliser de façon répétée, on a donc $c_0\geqslant\sqrt{a_0+b_0\xi_{n-1}^\sigma(0)}$ . Par conséquent,

$c_1=\cfrac{c_0^2-a_0}{b_0}\geqslant\xi_{n-1}^\sigma(0)=\sqrt{a_1+b_1\xi_{n-2}^{\sigma^2}(0)}$

Du coup,

$c_2=\cfrac{c_1^2-a_1}{b_1}\geqslant\xi_{n-2}^{\sigma^2}(0)=\sqrt{a_2+b_2\xi_{n-3}^{\sigma^3}(0)}$

De proche en proche, on vérifie ainsi que $c_k\geqslant\xi_{n-k}^{\sigma^k}(0)\geqslant 0$ pour $k=0,\ldots, n$ , ce que nous voulions établir.

La réciproque, à savoir $c_0,\ldots,c_n\geqslant 0$ entraîne $\gamma\geqslant u_n(\mathbf 0)$ , est très simple : si $c_n\geqslant 0$ , alors

$u_n(\mathbf 0)=\xi_n(0)\leqslant \xi_n(c_n)=u_n(c)=\gamma$

En conclusion, $c$ est à valeurs postives ou nulles et $u(c)$ est constant si, et seulement si, (3) et (4) sont vrais. Par conséquent :

–– si $u(\mathbf 0)$ converge vers un nombre réel $\gamma_0$ , alors (4) est vérifié par $\gamma=\gamma_0$ car la suite $u(\mathbf 0)$ est strictement croissante vu que

$u_{n+1}(0)=\xi_{n+1}(0)=\xi_n(\sqrt{a_n})>\xi_n(0)=u_n(\mathbf 0)$

La suite $c$ définie par (3) avec $\gamma=\gamma_0$ est donc à valeurs positives ou nulles et la suite $u(c)$ est constante.

–– inversement, s’il existe une suite $c$ à valeurs positives ou nulles telle que $u(c)$ soit constant, alors (4) est vérifié avec $\gamma=c_0=u_0(c)$ . Par conséquent, $u(\mathbf 0)$ converge vers un nombre réel $\gamma_0$ ne dépassant pas $\gamma$ .

Nous venons de prouver (2) et (3). Il nous reste à prouver (1).

Supposons donc que $u(\mathbf 0)$ ne converge pas vers un nombre réel et montrons par l’absurde qu’il tend vers $\infty$ . Comme cette suite est croissante, elle n’est pas bornée. Supposons alors qu’elle ne tende pas vers $\infty$ . Il existe donc un nombre $K$ qui majore tous les termes d’une de ses sous-suites, que nous noterons $u'$ . Comme $u(\mathbf 0)$ n’est pas borné, il existe un entier $n$ tel que $K<u_n(\mathbf 0)$ . D'où une contradiction car pour $m$ assez grand, $u_n(\mathbf 0)<u'_m\leqslant K$ .

Voilà, le théorème est prouvé!

Ce théorème me semble fournir des arguments sérieux en faveur de la définition de l'empilement $e(a,b)$ que nous avons adoptée dans le billet précédent, du moins pour des suites à valeurs strictement positives — le cas que nous considérons ici, à savoir poser

$\sqrt{a_0+b_0\sqrt{a_1+b_1\sqrt{a_2+b_2\sqrt{\cdots}}}}=\lim u(\mathbf 0)$

sous réserve que cette limite existe.

D’abord, le point 1) du résultat nous montre que cette limite existe toujours. Elle peut certes valoir $\infty$ alors qu’on espérerait que $e(a,b)$ soit un nombre réel mais cela ne me semble pas rédhibitoire.

Ensuite, les points 2) et 3) montrent que si cette limite est un nombre réel $\gamma_0$ , pour chaque $\gamma\geqslant \gamma_0$ , il y a une suite d’approximations qui converge syntaxiquement vers l’expression $e(a,b)$ mais dont les évaluations sont égales à $\gamma$ . Le nombre $\gamma_0$ est le plus petit possible ayant cette propriété et correspond à une suite d’évaluation syntaxiques

$\sqrt{a_0},\quad \sqrt{a_0+b_0\sqrt{a_1}}, \sqrt{a_0+b_0\sqrt{a_1+b_1\sqrt{a_2}}}, \quad \ldots$

raisonnables dont nous avons parlé dans le billet précédent. En raison de cela, s’il faut vraiment élire un de ces nombres $\gamma$ au titre de valeur de $e(a,b)$ , alors il me semble plus que normal de choisir $\gamma_0$ .

Cet argument est renforcé par l’observation suivante. En notant $c^\gamma$ la suite définie par la récurrence (3) et $\mathbf r$ la suite constante $n\mapsto r$ , on a

Si $\lim u(\mathbf 0)$ est un nombre réel $\gamma_0$ et si $c^{\gamma_0}$ converge vers $\infty$ , alors pour tout nombre réel positif $r$ , $\lim u(\mathbf r)=\gamma_0$ .

Sous les hypothèses de cette observation, on a en particulier $e(a,b)=\lim u(\mathbf 1)$ , ce qui correspond à l’autre suite d’approximations syntaxiques raisonnables rencontrée dans le billet précédent

$\sqrt{a_0+b_0}, \quad \sqrt{a_0+b_0\sqrt{a_1+b_1}}, \quad \sqrt{a_0+b_0\sqrt{a_1+b_1\sqrt{a_2+b_2}}}, \quad \ldots$

(C’est celle qu’on obtient en posant $e(\varepsilon,\varepsilon)=1$ .)

Voici comment justifier l’observation. Supposons que $c^{\gamma_0}$ converge vers $\infty$ . Alors il existe un seuil à partir duquel $r\leqslant c_n^{\gamma_0}$ . Au-delà de ce seuil, on a donc

$u_n(\mathbf 0)=\xi_n(0)\leqslant \xi_n(r)=u_n(\mathbf r)\leqslant \xi_n(c_n^{\gamma_0})= \gamma_0$

D’où la conclusion, par passage à la limite.

L’observation s’applique par exemple à l’empilement

$\sqrt{1+2\sqrt{1+3\sqrt{1+4\sqrt{\cdots}}}}$

dont j’ai parlé à plusieurs reprises. Pour celui-ci, en effet, $\gamma_0=3$ et $c^{\gamma_0} : n \mapsto n+3$ .

Cela dit, j’ai le sentiment qu’il existe un résultat plus fort que cette observation et que bien d’autres suites $c$ que celles de la forme $\mathbf r$ permettent de calculer l’empilement $e(a,b)$ . De nombreuses expérimentations informatiques m’en ont convaincu. Mais, pour l’heure, je n’ai encore rien trouvé de significatif.

Un exemple simple et amusant

Nous allons appliquer ce qui précède à l’empilement

$\sqrt{p+q\sqrt{p+q\sqrt{p+q\sqrt{\cdots}}}}$

Il est défini par les suites constantes $a=\mathbf p$ et $b=\mathbf q$ . Nous supposons bien entendu que $p$ et $q$ sont strictement positifs.

Nous allons voir que $\lim_{n\to \infty}u_n(\mathbf 0)$ est la racine positive de l’équation $t^2-qt-p=0$ , c’est-à-dire que

(5) $\boxed{\lim_{n\to \infty}\underbrace{\sqrt{p+q\sqrt{p+q\sqrt{\cdots + q\sqrt{p}}}}}_{n \mbox{\ lettres\ }p}=\cfrac{q+\sqrt{q^2+4p}}{2}}$

Voici comment. Appelons $\gamma$ cette racine. Il est facile de vérifier que la suite $c^\gamma$ définie par (3) est la suite constante $n\mapsto\gamma$ . Ses valeurs sont donc positives. D’après le théorème, $u(\mathbf 0)$ converge vers un nombre réel $\gamma_0\geqslant 0$ . On a alors, vu (1),

$u_{n+1}(\mathbf 0)=\xi_{n+1}(0)=\sqrt{p+q\xi_n^\sigma(0)}$

Mais, puisque les suites $a$ et $b$ sont constantes, $\xi_n^\sigma=\xi_n$ . Donc

$u_{n+1}(\mathbf 0)=\sqrt{p+qu_n(\mathbf 0)}$

En passant à la limite, il vient $\gamma_0=\sqrt{p+q\gamma_0}$ . Ainsi, $\gamma_0=\gamma$ , ce qui achève notre calcul.

Avec notre définition, nous sommes ainsi conduits à écrire

$\sqrt{p+q\sqrt{p+q\sqrt{p+q\sqrt{\cdots}}}}=\cfrac{q+\sqrt{q^2+4p}}{2}$

Lorsque $p=q=1$ , la limite (5) est le nombre d’or. Lorsque $p=2$ et $q=1$ , elle vaut $2$ . Cela nous le savions bien, sans peut-être en avoir pleinement pris conscience. En effet, j’ai signalé dans le billet précédent que

$\underbrace{\sqrt{2+\sqrt{2+\sqrt{\cdots + \sqrt{2}}}}}_{n \mbox{\ chiffres\ }2}=2\cos\cfrac{\pi}{2^{n+1}}$

😉

4 réactions sur “A propos des empilements infinis de radicaux III”

projetmbc dit :

14 octobre 2016 à 8:37

Merci pour ce billet avec l’exemple final très éclairant.

Réponse
- Pierre Lecomte dit :
  
  16 octobre 2016 à 9:55
  
  L’exemple final se généralise à des suites $a$ et $b$ périodiques de même période, $\ell$ . Il correspond à $\ell=1$ .
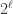  Mais le problème se complique très fort lorsque $\ell>1$ car l’équation satisfaite par la valeur de l’empilement est de degré $2^\ell$ .
  
  Réponse
Pingback: A propos des empilement infinis de radiaux V | Blog de Pierre Lecomte
Pingback: A propos d’un empilement infini de radicaux | Blog de Pierre Lecomte